10.Sınıf Matematik Dersi Formlarını İndirin!
2025-2026 eğitim öğretim yılı ilk kez yeni müfredata göre hazırlanan lise 10.sınıf matematik ders kitabındaki tüm formlara buradan kolayca ulaşabilirsiniz.

Lise Matematik 10 dersinin tüm temalarına ait ölçülmek istenen becerilerin değerlendirilmesi için “Grup değerlendirme formu“, “Akran değerlendirme formu” ve “Analitik dereceli puanlama anahtarı” formlarını buradan tek tıkla indirebilirsiniz.
Formların her biri, aslında ders kitabındaki karekod ile EBA dan indirilebiliyor ancak bu şekilde bir arada olması hem öğrencilerin hem de öğretmenlerin işini kolaylaştıracağını düşünüyoruz.
10.Sınıf Matematik Dersi 1.Tema Formları
1. Tema Performans Görevi 1 Analitik Dereceli Puanlama Anahtarı için TIKLAYIN
1. Tema Araştırma Ödevi Analitik Dereceli Puanlama Anahtarı için TIKLAYIN
1. Tema Performans Görevi 2 Grup Değerlendirme Formu için TIKLAYIN
1. Tema Performans Görevi 2 Akran Değerlendirme Formu için TIKLAYIN
1. Tema Performans Görevi 2 Analitik Dereceli Puanlama Anahtarı için TIKLAYIN
10.Sınıf Matematik Dersi 2.Tema Formları
2.Tema Uygulama İçi Öz Değerlendirme Formu için TIKLAYIN
2.Tema Uygulama İçi Akran Değerlendirme Formu için TIKLAYIN
2.Tema Uygulama İçi Veri Toplama Planı Kontrol Formu için TIKLAYIN
2.Tema Performans Görevi Grup Değerlendirme Formu için TIKLAYIN
2.Tema Performans Görevi Akran Değerlendirme Formu için TIKLAYIN
2.Tema Performans Görevi Analitik Dereceli Puanlama Anahtarı için TIKLAYIN
2.Tema İstatistiksel Araştırma Sorusu Ölçütleri Kontrol Formu için TIKLAYIN
10.Sınıf Matematik Dersi 3.Tema Formları
Önümüzdeki günlerde eklenmiş olacak…Bizi izlemeye devam edin..
10. Sınıf Matematik Grup Değerlendirme Formu, Akran Değerlendirme Formu ve Analitik Dereceli Puanlama Anahtarı
Yeni matematik müfredatında öğrencilerin yalnızca sınav sonuçlarıyla değil, süreç boyunca gösterdikleri performansla da değerlendirilmesi ön plana çıkıyor. Bu noktada grup değerlendirme formu, akran değerlendirme formu ve analitik dereceli puanlama anahtarı önemli araçlar olarak kullanılmaktadır.
Grup Değerlendirme Formu
Grup değerlendirme formu, öğrencilerin bir proje veya performans görevi üzerinde birlikte çalışırken nasıl iş birliği yaptığını ölçmek için kullanılır. Grup üyelerinin görev paylaşımı, katılım düzeyi ve sorumluluk bilinci bu formla değerlendirilir. Böylece öğrencilerin sadece bireysel başarıları değil, takım içindeki katkıları da görünür hâle gelir.
Akran Değerlendirme Formu
Akran değerlendirme formu, öğrencilerin birbirlerinin çalışmalarını önceden belirlenmiş ölçütlere göre değerlendirmesine imkân tanır. Bu yöntem sayesinde öğrenciler, eleştirel düşünme becerilerini geliştirir ve yapıcı geri bildirim verme alışkanlığı kazanır. Aynı zamanda öğrenciler, kendi eksiklerini başkalarının çalışmalarını değerlendirirken daha iyi fark eder.
Analitik Dereceli Puanlama Anahtarı
Analitik dereceli puanlama anahtarı, bir görevi veya projeyi ayrıntılı ölçütlere ayırarak değerlendirme imkânı sunar. Örneğin doğruluk, sunum, içerik ve düzen gibi başlıklar üzerinden puanlama yapılır. Böylece öğrenciler yalnızca toplam puan almakla kalmaz; hangi alanlarda başarılı olduklarını ve hangi alanlarda gelişmeleri gerektiğini de görebilir. Bu da sürecin daha adil, şeffaf ve öğretici olmasını sağlar.
Öğrenciler ve Öğretmenler İçin Önemi
- Öğrenciler için beklentiler daha net hâle gelir ve hangi ölçütlere odaklanmaları gerektiğini önceden bilirler.
- Öğretmenler için daha adil ve güvenilir bir değerlendirme ortamı oluşur.
- Grup ve akran değerlendirmesi öğrencilerin sorumluluk bilincini ve sosyal becerilerini artırır.
- Analitik puanlama sayesinde hem güçlü yönler hem de geliştirilmesi gereken alanlar kolayca ortaya çıkar.
✨ Sonuç olarak, bu üç araç 10. sınıf matematik derslerinde yalnızca bir ölçme-değerlendirme aracı değil, aynı zamanda öğrencilerin öğrenme sürecine aktif katılımını sağlayan birer rehberdir. Hem öğretmenler hem de öğrenciler için daha şeffaf, katılımcı ve adil bir değerlendirme süreci sunar.
10.Sınıf Matematik Kitabı Sayfa 54 Cevapları-Çözümü -MEB Yayınları
10.Sınıf Matematik Kitabı Sayfa 54 Cevapları –10.Sınıf Matematik ders kitabı “Üçgenin Yükseklikleri” ile ilgili Sayfa 54’deki 11.Sıra Sizde sorusunun cevabı, detaylı çözümü.
🔺 Üçgenin Yüksekliği Nedir?
Bir üçgende yükseklik, köşeden karşı kenara indirilen dik doğru parçasıdır.
- Üçgenin her köşesinden bir yükseklik çizilebilir.
- Bu yüzden her üçgenin 3 yüksekliği vardır.
- Yükseklikler üçgenin içinde, dışında veya kenar üzerinde kesişebilir.
- Yüksekliklerin kesiştiği noktaya diklik merkezi denir.
📌 Üçgen Türlerine Göre Yüksekliğin Durumu
- Dar açılı üçgende: Tüm yükseklikler üçgenin içinde kesişir.
- Dik üçgende: İki kenar zaten yükseklik olur, üçüncü yükseklik dik kenarların kesişim noktasından çizilir.
- Geniş açılı üçgende: Geniş açılı üçgenlerin yükseklikleri üçgenin dış bölgesinde kesişir.
10.Sınıf Matematik Ders Kitabı Sayfa 54 Sıra Sizde-11 Cevabı-Çözümü -MEB Yayınları
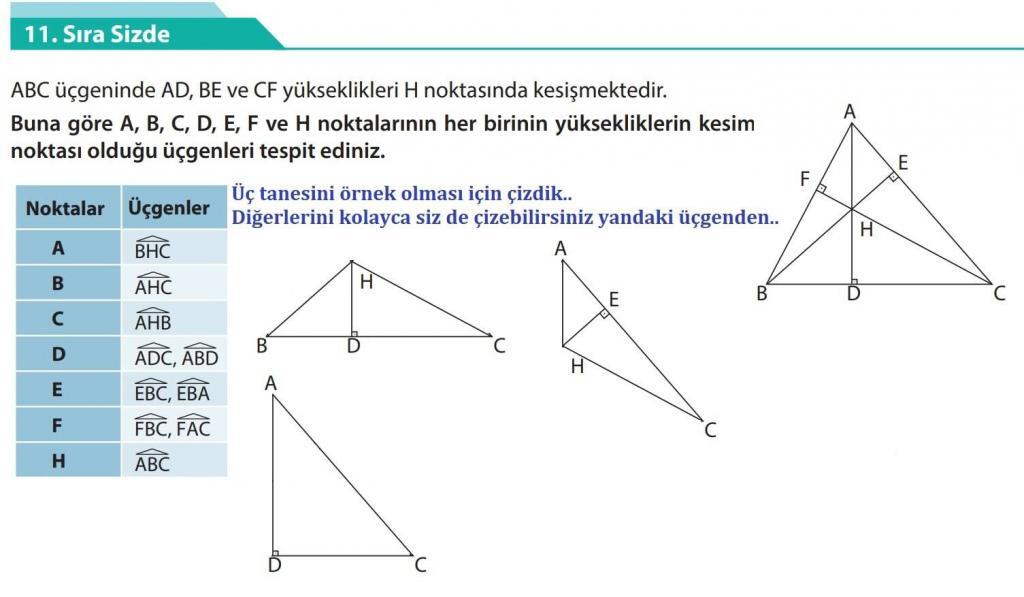
10. Sınıf Matematik Ders Kitabı Cevapları (MEB Yayınları)
10.Sınıf Matematik Kitabı Sayfa 51 Cevapları-Çözümü -MEB Yayınları
10.Sınıf Matematik Kitabı Sayfa 51 Cevapları –10.Sınıf Matematik ders kitabı “Üçgenin Kenar Orta Dikmeleri” ile ilgili Sayfa 51’deki 10.Sıra Sizde sorusunun cevabı, detaylı çözümü.
📌 Üçgenin Kenar Orta Dikmeleri
Bir üçgende, kenarların orta noktalarından kenarlara dik çizilen doğru parçalarına kenar orta dikme denir.
👉 Üç kenarın kenar orta dikmesi her zaman tek bir noktada kesişir.
👉 Bu nokta çevrel merkez olarak adlandırılır.
👉 Çevrel merkez, üçgenin köşelerinin hepsine eşit uzaklıktadır.
🔹 Önemli Sonuç:
Bu nokta, üçgenin çevrel çemberinin merkezidir. Yani üçgenin tüm köşelerinden geçen bir çember çizmek istersek, bu çemberin merkezi işte bu noktadır.
10.Sınıf Matematik Ders Kitabı Sayfa 51 Sıra Sizde-10 Cevabı-Çözümü -MEB Yayınları

Bir üçgende, herhangi bir kenarın orta noktasından geçen ve o kenara dik olan doğru parçasına kenar orta dikme denir.
👉 Kısaca:
Kenar orta dikmelerin kesişim noktası = Çevrel Çemberin Merkezi
10. Sınıf Matematik Ders Kitabı Cevapları (MEB Yayınları)
9.Sınıf Matematik Kitabı Sayfa 55-56 Cevapları-Çözümleri -MEB Yayınları
9.Sınıf Matematik Ders Kitabı Sayfa 55 ve Sayfa 56 Cevapları– 9.Sınıf Matematik 1. Ders kitabı “Aralıkların Mutlak Değer Gösterimi” konusuyla ilgili “Alıştırma” sorularının cevapları, ayrıntılı çözümleri burada
🔹 Mutlak Değerli Eşitsizlikler Nerelerde kullanılır?
- Eşitsizliklerde: Mesela ∣x−3∣<5 demek, “x sayısı 3’e en fazla 5 birim uzaklıkta” demektir. Bu da −2<x<8 anlamına gelir.
- Geometride: İki nokta arasındaki uzaklığı bulmak için.
- Günlük hayatta: Ölçüm yaparken ± hata payını göstermek için. Örneğin “bir cismin boyu 10 ± 0,5 cm” demek, boyun 9,5 cm ile 10,5 cm arasında olduğunu belirtir.
9.Sınıf Matematik 1.Ders Kitabı Sayfa 55 Alıştırma Soru Çözümleri -MEB Yayınları


9.Sınıf Matematik 1.Ders Kitabı Sayfa 56 Alıştırma Soru Çözümleri -MEB Yayınları


Mutlak değerli eşitsizlikler özeti için sayfa 54‘deki “Kontrol noktası” nı soruların çözümünden önce bakmanızda fayda var. Kitapta var ama yine de buradan aynen paylaşıyoruz.
9mat-mutlak-degerli-esitsizlik-araliklari-ozet-sayfa549.Sınıf Matematik Ders Kitabı Cevapları-Çözümleri – MEB Yayınları
9.Sınıf Matematik Kitabı Sayfa 52 Cevapları-Çözümleri -MEB Yayınları
9.Sınıf Matematik Ders Kitabı Sayfa 52 Cevapları- 1. Ders kitabı “Aralıkların Mutlak Değer Gösterimi” konusuyla ilgili Sayfa 52‘deki “12.Sıra Sizde” sorularının cevapları, ayrıntılı çözümleri burada
Aralıkların Mutlak Değer Gösterimi
Sayı doğrusu üzerinde iki nokta arasındaki uzaklığı göstermek için mutlak değer kullanılır. Örneğin, ∣a−b∣ ifadesi bize a ile b arasındaki mesafeyi verir. Yani aslında mutlak değer, “uzaklık” anlamına gelir.
🔹 Ne işe yarar?
- İki sayı arasındaki farkın uzaklık olarak gösterilmesini sağlar.
- Bir sayının belli bir aralıkta olup olmadığını kısa yoldan yazmamıza yardımcı olur.
- Eşitsizlikleri daha düzenli ve kolay yazmamıza imkan tanır.
👉 Kısacası, mutlak değer gösterimi aralıkları daha anlaşılır ve pratik şekilde ifade etmemizi sağlar.
9.Sınıf Matematik 1.Ders Kitabı Sayfa 52 Sıra Sizde-12 Soru Çözümleri -MEB Yayınları


Matematik 1. Ders kitabında yer alan, konunun özeti olan sayfa 54‘deki “Kontrol noktası” nı soruların çözümünden önce gözden geçirmenin faydalı olacağını söyleyelim.
9mat-mutlak-degerli-esitsizlik-araliklari-ozet-sayfa549.Sınıf Matematik Ders Kitabı Cevapları-Çözümleri – MEB Yayınları





