9.Sınıf matematik ders kitabında 2.Tema “Nicelikle ve Değişimler” konusunun özü doğrusal fonksiyonlar. Doğrusal fonksiyonların anlaşılabilmesi için bunların üretildiği “Doğrusal Referans Fonksiyonu” çok iyi anlaşılmalı. Bu nedenle bu dersimizde, 9.sınıf müfredatına göre, doğrusal referans fonksiyonu ve doğrusal referans fonksiyonunun nitel özellikleri ile ele alacağız.
Eğer doğrusal referans fonksiyonunun cebirsel temsili-grafiği ve özellikleri tam öğrenilirse reel sayılarda tanımlı doğrusal fonksiyon ve mutlak değer fonksiyonu çok daha rahat anlaşılır. Bu nedenle bu dersimizde bu fonksiyonu olabildiği kadar konuyu dağıtmadan, cebirsel temsilini ve grafiğini anlatacağız.
Doğrusal Referans Fonksiyonu Nedir?
Doğrusal referans fonksiyonun en belirgin özelliği, bağımsız değişken ile bağımlı değişken arasındaki ilişkinin birebir ve sabit oranlı olmasıdır. Yani x bir birim arttığında fonksiyon değeri de aynı şekilde bir birim artar. Eğim değeri 1 olduğundan fonksiyon her zaman sabit bir artış oranı gösterir. Sabit terimi 0’dır, bu nedenle grafik orijinden geçer ve koordinat sisteminde orijinden başlayarak 1 birim sağa gidildiğinde 1 birim yukarı çıkan bir doğru oluşturur. Bu fonksiyon hem süreklidir hem de tanım kümesindeki her gerçek sayı için değer alır. Ayrıca diğer bütün doğrusal fonksiyonların düşünülebileceği bir “temel model” görevi görür; çünkü diğer doğrusal fonksiyonlar, bu referans fonksiyonun eğiminin ve sabit teriminin değiştirilmiş hâlleri olarak düşünülebilir. Bu nedenle doğrusal davranışların anlaşılması için başlangıç noktası niteliği taşır. Bu nedenle doğrusal fonksiyonların çok iyi anlaşılması için bu fonksiyon çok iyi bilinmeli.
Örnek: Bir dijital ekran, üzerine yazılan x değerlerini anında y’ değerlerine dönüştürmektedir. Ekranın dönüşüm kuralı doğrusal referans fonksiyonudur. Ekrana sırasıyla –2, 0, 7 değerleri girildiğinde ekranda hangi sonuçlar görünür?
Cevap: f(x)=x olduğu için f(-2)=-2 , f(0)=0 , f(7)=7
Kısaca, özel bir doğrusal fonksiyon olan f(x)=x şeklinde tanımlı fonksiyona doğrusal referans fonksiyon denir. Diğer doğrusal fonksiyonlar bu referans fonksiyondan “türetilmiş” gibi düşünülebilir. Örnek: f(x)=x+2, g(x)=3x-1 vb..
Günlük hayatta doğrusal ilişkileri ifade etmek için doğrusal fonksiyonlar kullanılır. Bu nedenle bu konu hayatla oldukça ilgili bir konu. Zaten bu konuyla ilgili günlük hayatın içinden örneklere de yer verilir.
Gerçek hayattaki iki değişken arasındaki doğrusal bağlantı, doğrusal fonksiyonlar aracılığıyla gösterilebilir. Bu tür fonksiyonların grafikleri, bir kartezyen koordinat sisteminde her zaman bir doğruyu temsil eder. Fonksiyonların hem cebirsel (denklem) hem de grafiksel gösterimlerini kullanarak, bu doğrusal ilişkiden çeşitli çıkarımlar yapmak mümkündür.
Doğrusal Referans Fonksiyonunun Nitel Özellikleri:
– Tanım kümesi,
– Görüntü kümesi,
– İşareti,
– Artanlığı-azalanlığı,
– Maksimum-minimum noktaları,
– Sıfırı
– Bire birliği
Tanım Kümesi: Bir fonksiyonda bağımsız değişkenin (x) kabul edebileceği tüm değerlerin kümesine tanım kümesi denir. Giriş değerlerinin oluşturduğu kümedir. Kısaca x’in yerine yazılabilecek değerlerin kümesi.
Görüntü Kümesi: Tanım kümesindeki her değere karşılık bağımlı değişkenin (f(x)=y) aldığı tüm değerlerin oluşturduğu küme, görüntü kümesidir. Fonksiyonun ürettiği çıktı değerleri kümesidir.
Cebirsel temsili f(x)= x olan f fonksiyonunda x, tüm gerçek sayı değerlerini alabilir. Bu sebeple f fonksiyonunun en geniş tanım kümesi gerçek sayılardır. f fonksiyonu, x in aldığı tüm gerçek sayı değerlerini kendisi ile eşleştirir. Bu sebeple
f fonksiyonunun görüntü kümesi gerçek sayılardır. Buradan f fonksiyonu, f: R—–>R şeklinde tanımlanır.
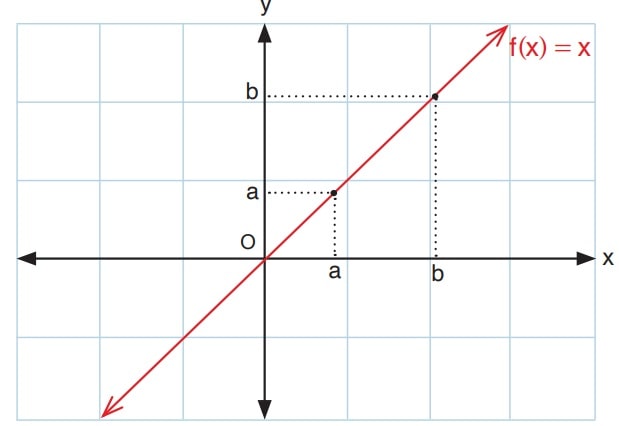
İşareti: f(x)=x fonksiyonunun işareti x>0 için pozitif, x<0 için negatiftir. Grafik incelendiğinde x > 0 iken f(x) in pozitif değerler aldığı, x < 0 iken f(x) in negatif değerler aldığı görülür
Artanlığı-azalanlığı: Her a ve b reel sayıları için, a < b iken f(a)<f(b) oluyorsa f, gerçek sayılarda artan; a < b iken f(a)>f(b) oluyorsa f, gerçek sayılarda azalan fonksiyondur. Şöyle de ifade edebiliriz;
Fonksiyonun tanımlı olduğu belirli bir aralık için bağımsız değişkenin aldığı değerler artarken bağımlı değişkenin aldığı değerler de artıyorsa fonksiyon bu aralıkta artandır.
Fonksiyonun tanımlı olduğu belirli bir aralık için bağımsız değişkenin aldığı değerler artarken bağımlı değişkenin aldığı değerler azalıyorsa fonksiyon bu aralıkta azalandır.
Gerçek sayılarda f(x) = x şeklinde tanımlı f doğrusal referans fonksiyonunda bağımsız değişkenin aldığı değerler artarken bağımlı değişkenin aldığı değerler de artmaktadır, aldığı değerler azalırken bağımlı değişkenin değerleri azalmaktadır. Bu nedenle f(x) = x doğrusal referans fonksiyonu artandır.
Maksimum-minimum noktaları: Reel sayılarda tanımlı f(x)=x doğrusal referans fonksiyonunun maksimum ve minimum noktası yoktur. Eğer tanım ve değer kümeleri belli bir aralıksa bu durumda maksimum ve minimum noktaları olabilir.
Fonksiyonun sıfırı: f fonksiyonunda f(x)= 0 eşitliğini sağlayan x değerine f fonksiyonunun sıfırı denir. Grafik incelendiğinde x = 0 için f(0) = 0 olduğu görülür. Buna göre, f(x) = x fonksiyonunun sıfırı 0 (sıfır) dır.
Bire birliği: Bir f fonksiyonunda tanım kümesinde farklı x değerlerine karşılık gelen f(x) değerleri birbirinden farklı ise f, bire bir fonksiyondur. Benzer şekilde görüntü kümesindeki bir f(x) değerine tanım kümesinde sadece bir x değeri karşılık geliyorsa f, bire bir fonksiyondur. Bu nedenle f(x)=x doğrusal referans fonksiyonu bire birdir.
9.sınıf matematik 1.ders kitabında konu özeti şu şekilde yer alıyor:

Doğrusal Referans Fonksiyonuyla İlgili Örnekler
Örnek-1:Bir öğrenci, “f(x)=x fonksiyonunda bağımlı değişken her zaman bağımsız değişkenden 1 fazladır.” demiştir. Bu öğrencinin hatasını örneklerle açıklayınız.
Cevap: Fonksiyonda bağımlı değişken bağımsız değişkene eşittir. f(2)=2, f(5)=5, f(–4)=–4. Hiçbirinde bağımlı değişken bağımsız değişkenden 1 fazla değildir. Yanlış yorum: “x+1” şeklindeki fonksiyonla karıştırmıştır.
Örnek-2: Ali, yürüyüş bandında hızı 1 km/s olacak şekilde koşmaktadır.bGeçen süre x (saat), koştuğu mesafe f(x) olmak üzere ilişki doğrusal referans fonksiyonuna benzemektedir.
a) Fonksiyonu yazınız.
b) 2,5 saatte kaç km koşar?
c) Bu durum neden doğrusal referans fonksiyonu ile modellenebilir?
Cevap:
a) Hız: 1 km/s → mesafe = zaman f(x)=x
b) f(2.5)=2.5 km,
c) Çünkü her saat mesafe 1 km artar. Artış sabittir ve birebir ilişki vardır → bu, f(x)=x yapısına uygundur.
Örnek-3: Şu bilgi f(x)=x fonksiyonuna aittir: x değeri 7’den 12’ye çıkmıştır. Buna göre;
a) x kaç birim artmıştır?
b) f(x) kaç birim artmıştır?
c) Bu sonuç doğrusal referans fonksiyonunun hangi özelliğini gösterir?
Cevap:
a) 12 – 7 = 5 birim
b) Fonksiyonda artış x artışıyla aynıdır → 5 birim
c) Fonksiyonun değişim oranı (eğim) 1’dir; x kadar artar, f(x) de aynı miktarda artar.
Ali SANCI-Matematik Öğretmeni