9.Sınıf Matematik Kitabı-1 Sayfa 92-93 Çözümleri -Doğrusal Referans Fonksiyon

9.Sınıf Matematik 1. Ders kitabı 2. Tema Nicelikler ve Değişimler “Gerçek sayılarda tanımlı doğrusal fonksiyonlar ve nitel özellikleri-Doğrusal Referans Fonksiyon” ile ilgili Sayfa 92 ve Sayfa 93 ‘deki “1.Uygulama” sorularının cevapları, ayrıntılı çözümleri burada

Uygulama ile Sayfa 92 ve Sayfa 93‘de de yer alan doğrusal referans fonksiyonu ile ilgili öğreneceklerimizi özetleyelim;

Bir fonksiyonda bağımsız değişkenin alabileceği tüm değerler, fonksiyonun tanım kümesi olarak adlandırılır. Bağımsız değişkenin alabileceği tüm değerlere karşılık bağımlı değişkenin alabileceği tüm değerler, görüntü kümesi olarak adlandırılır.

Cebirsel temsili f(x) = x olan doğrusal referans f fonksiyonunda x, tüm gerçek sayı değerlerini alabilir. Bu sebeple f fonksiyonunun en geniş tanım kümesi gerçek sayılardır. f fonksiyonu, x  in aldığı tüm gerçek sayı değerlerini kendisi ile eşleştirir. Bu sebeple f fonksiyonunun görüntü kümesi gerçek sayılardır. f fonksiyonu R den R ye tanımlıdır.

f fonksiyonunda f(x) = 0 eşitliğini sağlayan x değerine f fonksiyonunun sıfırı denir.

Her a ve b reel sayıları için;
a < b iken f(a)<f(b) oluyorsa f, gerçek sayılarda artan;
a < b iken f(a)>f(b) oluyorsa f, gerçek sayılarda azalan fonksiyondur

9.Sınıf Matematik Kitabı-1 Sayfa 92 ve Sayfa 93 1.Uygulama Cevapları- Çözümleri -MEB Yayınları

Gerçek Sayılarda f(x)=x Şeklinde Tanımlı f Doğrusal Referans Fonksiyonunun Nitel Özellikleri

Verilen bilgileri inceleyerek soruları cevaplayınız.

1. Sabit hızla hareket eden bir araç, dakikada 1 kilometre yol almaktadır. Araç, sabit hızla 120 dakika boyunca hareket etmiş ve 120 km yol almıştır. Aracın harekete başladığı andan itibaren zamana (dk.) bağlı aldığı mesafeyi (km) gösteren fonksiyon g olmak üzere g fonksiyonunun cebirsel temsili, g(x) = x olur. Aşağıda f fonksiyonunun grafiği verilmiştir.

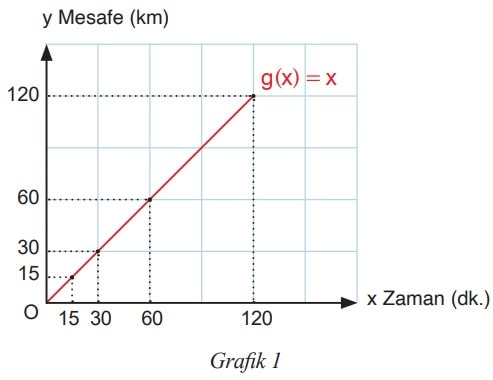
a) Aşağıdaki tabloda bağımsız değişkenin (x) aldığı bazı değerlere karşılık gelen bağımlı değişken (g(x))
değerleri verilmiştir. Tabloda verilmeyen değerleri bulunuz.

b) Bağımlı değişkenin minimum (en küçük) ve maksimum (en büyük) değerini bulunuz.

Bağımlı değişkenin en küçük değeri 0, en büyük değeri 120

b) Bağımlı ve bağımsız değişkenlerin alabileceği değerlerin aralıklarını bulunuz.

Her ikisinin de alabileceği değer aralığı [0,120]

ç) Bağımsız değişkenin hangi değeri için bağımlı değişkenin sıfıra eşit olduğunu bulunuz.

g(x) = x olduğundan: x=0 için g(0)=0

d)Bağımlı değişken; bağımsız değişkenin hangi değerleri için pozitif, hangi değerleri için negatif olur? Bulunuz.

Bağımlı değişken(y), bağımsız değişken(x) in sıfırdan farklı tüm değerleri için her zaman pozitif olur. Negatif olamaz. Yani x ∈ [0,120] olduğu için negatif değer yoktur. g(3)=3, g(7/2)=7/2 …

e) Bağımsız değişkenin aldığı değerler artarken g fonksiyonunun aldığı değerlerin nasıl değiştiğini belirleyiniz.

Bağımsız değişkenin aldığı değerler artarken g fonksiyonunun aldığı değerlerde artar. Yukarıdaki tabloda bu durum zaten net olarak görülüyor.

f) Bağımsız değişkenin aldığı iki farklı değer için g fonksiyonunun aldığı değerler birbirinden farklı mıdır? Bu durumun bağımsız değişkenin alabileceği tüm değerler için geçerli olup olmadığını açıklayınız

Farklıdır. Tüm değerler içinde geçerlidir. Çünkü g(x)=x olduğu için parantez içindeki x değiştikçe buna bağlı olan g(x)=x olarak değişir.

2. 1. maddede incelenen g fonksiyonu gerçek sayılarda tanımlanarak cebirsel temsili f(x) = x olan f doğrusal referans fonksiyonu elde edilmiştir. Grafik 2’de f doğrusal referans fonksiyonunun grafik temsili verilmiştir.

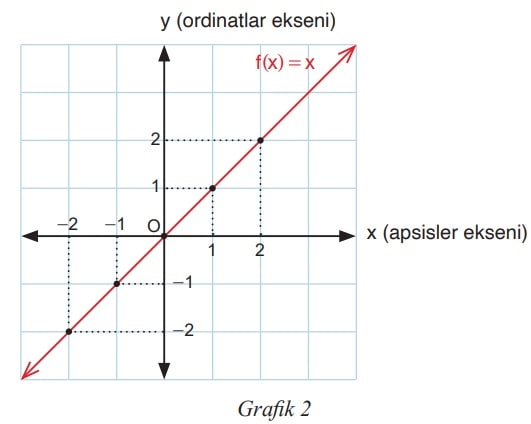
a) Tablo 2’de f doğrusal referans fonksiyonunda x e bağlı f(x) in aldığı bazı değerler verilmiştir. Verilmeyen değerleri bularak tabloda ilgili yerlere yazınız.

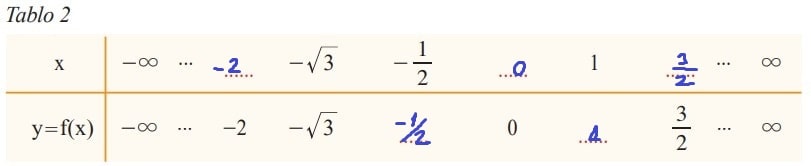
b) Bağımlı ve bağımsız değişkenlerin alabileceği değerlerin aralığını bulunuz.

Her ikisi de sonsuz değer alır. Yani x ve f(x) aldığı değer aralığı (∞,∞)

c) f fonksiyonunda f(x) = 0 eşitliğini sağlayan x değerini bulunuz.

f(x) = 0 eşitliğini sağlayan x=0 değeridir.

ç) Bir fonksiyonda bağımlı değişken; bağımsız değişkenin bazı değerleri için pozitif, bazı değerleri için negatif olabilir. Tablo 3’te f fonksiyonunun aldığı negatif ya da pozitif değerler belirlenecektir. Tablonun ilk satırı bağımsız değişkenin 2. satırı bağımlı değişkenin aldığı değerleri temsil etmektedir. İlk satırdaki alana f fonksiyonunda f(x) = 0 eşitliğini sağlayan x değerini yazınız. f fonksiyonunun negatif ya da pozitif olduğu aralıkları belirleyerek ikinci satırdaki ilgili alanlara yazınız.

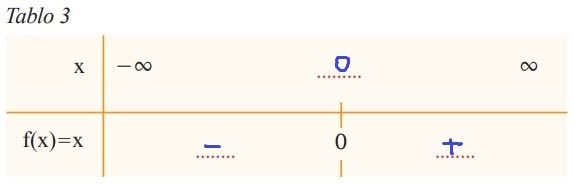
Şimdi de Doğrusal Referans Fonksiyon Hakkında Temel Bilgileri Özetleyelim:

Doğrusal Referans Fonksiyonunun Temel Özellikleri

*Doğrusal fonksiyonlarda değişim hızı sabittir. Yani x her birim arttığında, f(x) de aynı miktarda artar veya azalır.

Örneğin:

• f(x) = x ise fonksiyon her 1 artışta yine 1 artar.
• f(x) = 2x + 3 ise fonksiyon her 1 artışta 2 artar.

*Doğrusal fonksiyon grafiği koordinat düzleminde dümdüz bir doğru oluşturur. Eğim pozitifse doğru yukarı yönlü,
Eğim negatifse aşağı yönlü ilerler.

*Doğrusal fonksiyonlar günlük hayatta sabit hız, sabit fiyat artışı, sabit akış gibi durumları modellemek için kullanılır. Örneğin:

• Sabit hızla giden bir aracın zamana bağlı aldığı yol,
• Bir ürünün tanesi belli bir fiyattan satılıyorsa toplam ücret,
• Bir musluğun sabit hızla bir depoyu doldurması.

Bu tür durumlarda bağımsız değişken “zaman” veya “miktar”, bağımlı değişken ise “mesafe”, “ücret”, “hacim” gibi nicelikler olur.

*Eğim pozitifse:

• x arttıkça f(x) artar,
• x azaldıkça f(x) azalır.

Eğim negatifse:

• x arttıkça f(x) azalır.

Bu yüzden fonksiyonun hangi bölgelerde pozitif veya negatif olduğu, kesim noktaları incelenerek bulunabilir.

*“Doğrusal referans fonksiyonu” ifadesi özellikle matematik eğitiminde şu amaçla kullanılır:

• Öğrencilerin diğer fonksiyonları tanımlarken karşılaştırma yapabileceği temel bir model oluşturmak,
• Problemlerde değişimin sabit olduğu en basit durumu örnek göstermek.

Örneğin f(x) = x fonksiyonu, eğimi 1 olan bir referans fonksiyondur. Bu fonksiyon, “x ne kadar artarsa f(x) de o kadar artar” ilkesini temsil eder.

ÖZETLE;

Doğrusal referans fonksiyonu:

• Sabit değişim gösteren,
• Grafiği bir doğru olan,
• Pek çok gerçek yaşam durumunu modelleyen,
• Matematikte diğer fonksiyon türleri için başlangıç ve karşılaştırma modeli oluşturan temel bir fonksiyon türüdür.

Gerçek Sayılarda g(x)=a f(x±r)±k Şeklinde Tanımlı Doğrusal Fonksiyonlar:

a, r ve k birer reel sayı ve a ≠ 0 olmak üzere gerçek sayılarda f(x) = x şeklinde tanımlı f doğrusal referans fonksiyonundan türetilen ve g(x) = a f(x ± r) ± k şeklinde ifade edilen fonksiyonlara doğrusal fonksiyon denir.

Doğrusal fonksiyonların grafikleri, bir doğru belirtir ve f(x) = x şeklinde tanımlı doğrusal referans fonksiyondan türetilen fonksiyonlardan elde edilebilir.

9.Sınıf Matematik Ders Kitabı Cevapları-Çözümleri – MEB Yayınları