8.Sınıf Matematik Ders Kitabı Sayfa 95 “Ondalık İfadelerin Karekökleri” ile ilgili alıştırma sorularının cevapları, detaylı çözümleri, sonuç yayınları
•Tam kare tam sayıların kareköklerinin değeri doğal sayıdır. Devirli ondalık gösterimlerde devreden sayılar, üzerlerine çizgi konularak belirtilir.
•İki tam sayının oranı (a/b, a tam sayı ve b sıfırdan farklı bir tam sayı) olarak yazılabilen sayılara rasyonel s ayılar, yazılamayan sayılara irrasyonel sayılar adı verilir. Tam kare olmayan bir sayının karekökü irrasyonel sayıdır.
Devirli ondalık sayılar rasyonel sayıdır.
Devirli Ondalık Sayıları Rasyonel Olarak Yazma – Formül

Örnekler:
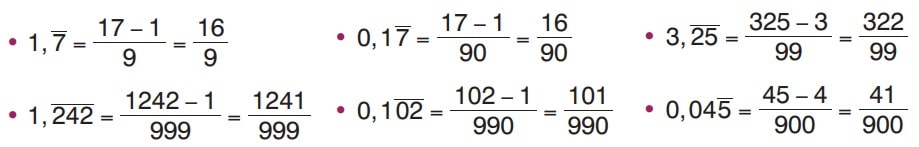
8.Sınıf Matematik Ders Kitabı Sayfa 95 Cevapları – Çözümleri – Sonuç Yayınları



İrrasyonel sayı: Rasyonel olmayan, yani tam sayı oranı şeklinde yazılamayan, düzensiz, sonsuz ondalıklı sayılardır.
Ondalık kısmı düzensiz (devretmiyor) ve sonsuza kadar devam eden ondalık yazılmış sayılar irrasyoneldir.
Pi sayısı, ondalık açılımı devretmeyen ve sonsuza kadar giden meşhur bir irrasyonel sayıdır.
Tam kare olmayan bir sayının karekökü irrasyoneldir.
✍️ Devirli Sayılar Hakkında Sözel Bilgi
Devirli sayılar, matematikte rasyonel sayılar kümesine ait olan ve ondalık gösteriminde virgülden sonra belirli bir rakamın ya da rakam grubunun sonsuza kadar düzenli bir şekilde tekrar etmesiyle oluşan özel bir ondalık sayı türüdür.
Bu tekrar eden rakam ya da rakam grubuna “devir” adı verilir. Devir kısmı, sayının ondalık yazılımında tekrar etmeye başladığı yerden itibaren geçerlidir. Devirli sayıları yazarken, tekrar eden basamakların üzerine yatay bir çizgi (devir çizgisi) konulur. Bu işaret, o rakamın veya rakam grubunun sonsuza dek kendini tekrar ettiğini belirtir ve sayının kısa ve net bir biçimde ifade edilmesini sağlar.
Örneğin:
- 1/3 kesrinin ondalık gösterimi 0,3333…şeklindedir ve 0,3 olarak yazılır. Burada devreden kısım 3‘tür.
- 4/11 kesri 0,363636… şeklindedir ve 0,36 olarak yazılır. Burada devreden kısım 36‘dır.
- 7/12 kesri 0,583333…şeklindedir ve 0,583 olarak yazılır. Burada devreden kısım 3‘tür, ancak 58 devir öncesi kısımdır.
🧐 Temel Özellikleri
- Rasyonel Sayı Olmaları: Tüm devirli sayılar, aslında birer rasyonel sayıdır. Bu, onların her zaman bir a/b (b sıfırdan farklı) kesri olarak ifade edilebileceği anlamına gelir. Bu da devirli sayıları, ondalık kısımları ne sonsuz ne de devirli olan irrasyonel sayılardan (örneğin pi veya kök 2) kesin olarak ayırır.
- Ondalık Gösterim: Bir kesrin devirli ondalık sayıya dönüşüp dönüşmeyeceği, kesrin sadeleştirilmiş halinin paydasındaki asal çarpanlara bakılarak anlaşılabilir. Eğer paydada 2 ve 5 dışında bir asal çarpan varsa (örneğin 3, 7, 11 gibi), bu kesrin ondalık gösterimi devirli olmak zorundadır.
- Kesre Çevirme: Devirli sayıların rasyonel sayı olduğunu kanıtlayan en önemli özellik, özel bir formül kullanılarak kolaylıkla kesir haline çevrilebilmeleridir.
Devirli sayılar, matematikte hem temel aritmetikte hem de daha ileri konularda, özellikle limit ve seriler gibi alanlarda önemli bir yere sahiptirler ve rasyonel sayılar kümesinin tam olarak anlaşılması için kritik öneme sahiptirler.
8.Sınıf Matematik Ders Kitabı Cevapları-Çözümleri- Sonuç Yayınları
[…] 8.Sınıf Matematik Kitabı Sayfa 95 Cevapları – Devirli Sayılar […]