8.Sınıf matematik konularından köklü sayılarda toplama ve çıkarma işlemleri ile ilgili Sonuç yayınlarına ait Sayfa 84 ve 85 deki alıştırma soruları cevapları, ayrıntılı çözümleri.
Alıştırmaları bitirince, aşağıda konuyu özetleyip ayrıca “Köklü sayılarda yapılan yaygın hatalara” değindik. Hata yapmamak için aşağıdaki bu yazımınız da okumanızı öneriyoruz. Sınavı kazandıran aslında çoğu kişinin yaptığı hatayı kişinin yapmamasıdır.
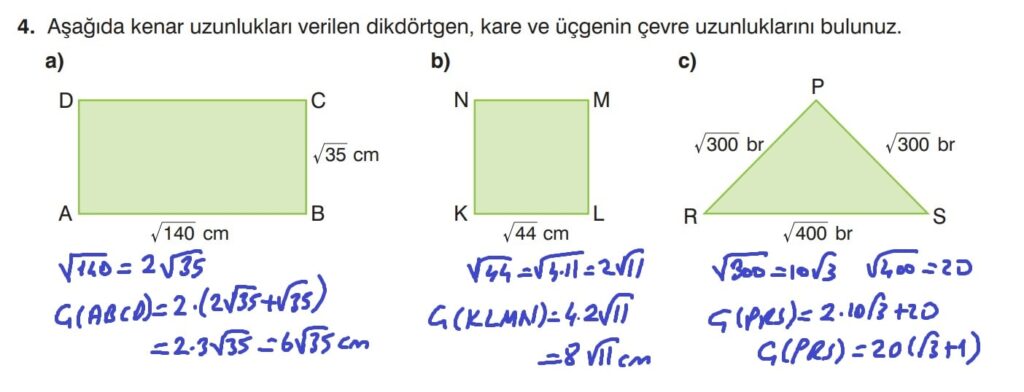
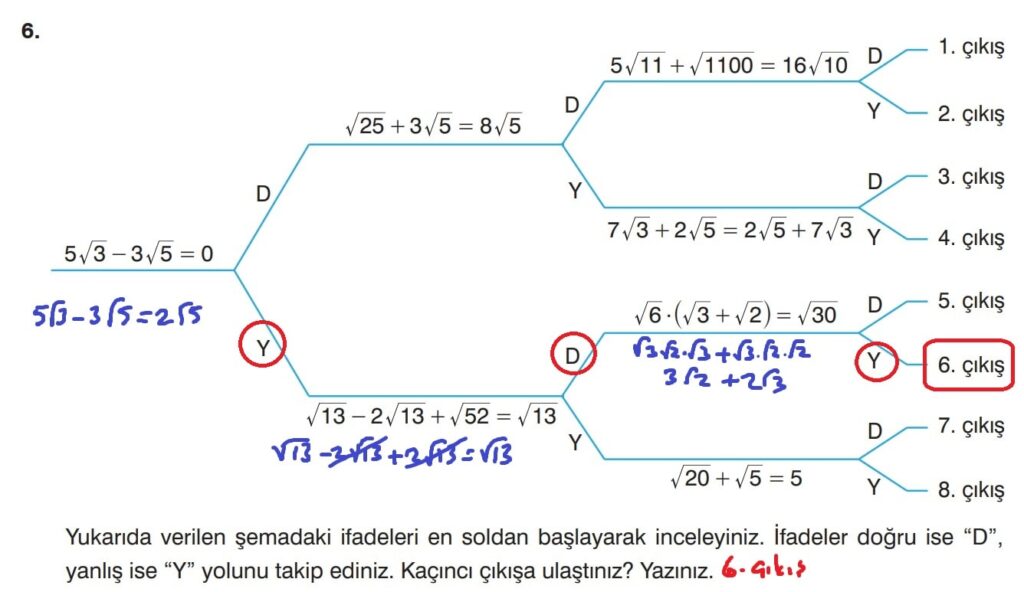
8.Sınıf Matematik Ders Kitabı Sayfa 84-85 Cevapları, Çözümleri -Sonuç Yayınları




🍎 Köklü Sayılarda Toplama ve Çıkarma İşlemi Özeti (8. Sınıf)
Köklü sayılarla toplama ve çıkarma yapmak, aslında aynı cinsten şeyleri bir araya getirmeye veya ayırmaya benzer. Tıpkı 3 elma ile 2 elmayı toplayıp 5 elma bulmak gibi düşünebilirsiniz.
Temel Kural: Kök İçlerinin Aynı Olması Şartı
Köklü sayılarda toplama veya çıkarma yapabilmeniz için, kök işaretinin içindeki sayının tamamen aynı olması gerekir. Bu kural, elmaların aynı türden olması şartı gibidir.- Eğer kök içindeki sayılar aynıysa: O zaman sadece kökün dışındaki sayıları (yani katsayıları) toplar veya çıkarırsınız. Ortak olan köklü ifadeyi sonucun yanına aynen yazarsınız.
Örneğin: Beş tane √7 ile iki tane √7’yi toplarsanız, toplamda yedi tane √7’niz olur.
Eğer kök içindeki sayılar farklıysa: Bu durumda direkt toplama veya çıkarma yapamazsınız. Tıpkı 3 elma ile 2 portakalı toplayıp “5 elma-portakal” diyemeyeceğiniz gibi.
Kök İçleri Farklıysa Ne Yapılır? (Kök Dışına Çıkarma)
İşlem yapmaya başlamadan önce, kök içindeki sayıları en sade hale getirmeniz gerekebilir. Bu, bir nevi büyük sayıyı parçalayıp, kök dışına çıkabilen kısmı çıkarmak demektir.
Bazen sayının bir kısmını kök dışına çıkararak, farklı görünen köklerin aslında aynı cinsten olduğunu fark edersiniz.
Örneğin: √12 başta √3’ten farklı görünür. Ama √12’yi sadeleştirdiğinizde (4 dışarı 2 olarak çıkar), aslında 2√3 olduğunu görürsünüz. Artık 2√3 ile 5√3’ü toplayabilirsiniz, çünkü kök içleri (√3) aynı olmuştur.
🛑 Köklü Sayılarda Yapılan Yaygın Hatalar
- Kök İçlerini Toplamak/Çıkarmak: En büyük hata budur. Öğrenciler √4 + √5 işlemini √9 olarak düşünürler. Bu KESİNLİKLE yanlıştır! Kök içleri farklıysa, direkt toplama yapılamaz. Toplama/çıkarma sadece katsayılar arasında yapılır, kök içi değişmez (aynı olmak şartıyla).
- Sadeleştirmeyi Unutmak: Kök içindeki büyük sayıları sadeleştirmeden “kök içleri farklı” deyip işlemi bırakmak da yaygın bir hatadır. İşlem yapmadan önce her zaman köklü ifadeyi en sade haline getirdiğinizden emin olun.
- Katsayısı Olmayanı “Sıfır” Sanmak: √5 gibi bir ifadenin önünde bir sayı yoksa, bu aslında “sıfır tane √5” anlamına gelmez. Tıpkı “x”in önünde 1 olması gibi, bunun da katsayısı 1‘dir.
8.Sınıf Matematik Ders Kitabı Cevapları-Çözümleri- Sonuç Yayınları
[…] 8.Sınıf Matematik Kitabı Sayfa 84-85 Cevapları-Sonuç Yayınları […]