10.Sınıf Matematik Kitabı Sayfa 98-99 1.Uygulama – İstatistiksel Bağlam Oluşturma

10.Sınıf Matematik 2.Tema İstatistiksel Araştırma Sürecinin ilk konusu “İki Kategorik Değişkenin İlişkililiğini İçeren İstatistiksel Problemi Oluşturma, Veri Toplama, Analiz Etme Ve Yorumlama” ile ilgili temel hususları özetlemeye çalışacağız. Bunu yaparken de 10.sınıf matematik ders kitabı Sayfa 98 ve Sayfa 99 daki bilgilerden yararlanarak soruları cevaplandıracağız.

Kategorik Değişken : Birbirine ortak özelliklerine göre sınıflandırılan ve belirli grup ya da kategoriler altında toplanan verilere kategorik değişken denir. (Cinsiyet, eğitim düzeyi, spor tercihi gibi.)

Bağlam: İstatistiksel araştırmalarda bağlam, verilere dayalı bilgi üretme ihtiyacı duyulan gerçek yaşam durumlarıdır.
Bağlam;
a) Verilerin toplanma koşullarını
b) İncelenen değişkenleri
c) Araştırmanın amacını,
anlamamızı sağlar.

Bağlamı belirlemeden yapılan analizler, yanlış yorumlamalara ve yanıltıcı sonuçlara yol açabilir.

10.Sınıf Matematik Ders Kitabı Sayfa 98 Cevabı

Genellikle sayısal verileri görselleştirmek için kullanılan çizgi grafiği, nokta grafiği, kök-yaprak gösterimi, histogram ve kutu grafiği gibi araçlar kategorik değişkenler arasındaki ilişkileri incelemek için de kullanılabilir mi?

Genel olarak hayır.
Çizgi grafiği, nokta grafiği, kök–yaprak gösterimi, histogram ve kutu grafiği esas olarak sayısal (nicel) veriler için geliştirilmiş gösterim türleridir. Bu grafiklerde:

• Veri değerlerinin sıralı olması,
• Sayısal aralıkların anlamlı olması,
• Hesaplamalara dayalı özetlerin (ortalama, medyan, dağılım genişliği vb.) kullanılabilmesi

gerekir.

Kategorik değişkenler ise bu tür sayısal düzenlemeleri gerektirmez ve çoğu zaman buna uygun değildir.

Uygun olmama nedenleri:

• Çizgi grafiği, noktaları sıralı bir nicel değişken üzerinden birleştirir. Kategorik değerler sıralı olmadığından çizgi grafiği anlamlı sonuç vermez.
• Histogram sınıflara ayrılmış sayısal veri gerektirir. Kategoriler için “sınıf aralığı” oluşturulamaz.
• Kutu grafiği, medyan ve çeyrek değerler gibi sayısal özetlere dayanır, kategorik verilere uymaz.
• Kök–yaprak grafiği tamamen sayısal veriler için geliştirilmiştir.
• Nokta grafiği, bazı durumlarda kategoriler için kullanılabilse de (örneğin frekansları göstermek için), temel olarak sayısal eksen üzerine yerleştirmeye dayanır.

Kategorik değişkenler için daha uygun grafikler

• Sütun grafiği (bar chart)
• Pasta grafiği
• Yüzdelik dağılım grafikleri
• Sayım (frekans) tabloları

Bu grafikler kategorik değişkenler arasındaki ilişkileri göstermede daha anlamlıdır.

Kısaca; Sayısal veri grafiklerinin çoğu, kategorik değişkenler arasındaki ilişkileri incelemek için uygun değildir. Bu nedenle kategorik veriler için özel olarak geliştirilmiş grafik türleri tercih edilmelidir.

10.Sınıf Matematik Ders Kitabı Sayfa 99 – 1.Uygulama

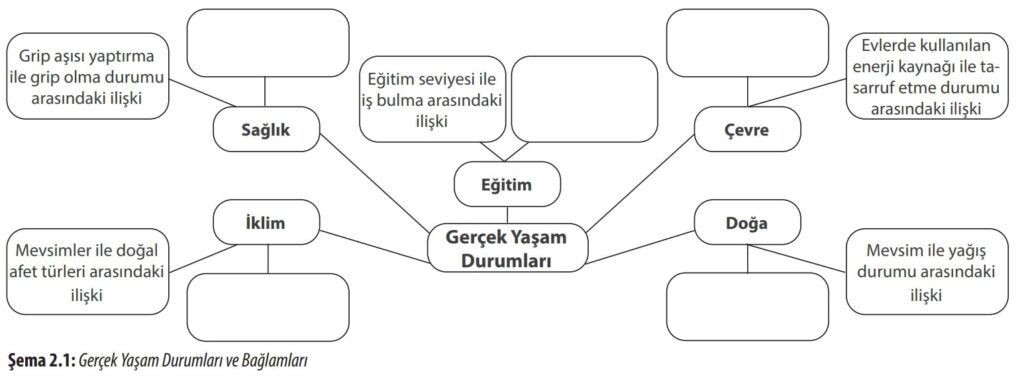
a) Şemada verilen bağlamların iki kategorik değişkenli veri toplamayı gerektiren bağlamlar olmasının nedeni ile ilgili olarak grup arkadaşlarınızla tartışınız.

Şemada verilen her bağlam, iki farklı özelliğin (iki kategorik değişkenin) birbiriyle ilişkisini incelemeyi gerektirir.
Bu özelliklerin ikisi de sınıflara ayrılan, yani sayısal olmayan kategorik değişkenlerdir.

Örneğin:

• Grip aşısı yaptırma durumu (yaptırdı / yaptırmadı) ve
  Grip olma durumu (oldu / olmadı)
  → Her ikisi de kategoriktir. İlişkiyi görmek için veri toplamak gerekir.
• Eğitim seviyesi (ilkokul / lise / üniversite …) ve
  İş bulma durumu (buldu / bulamadı)
  → Her ikisi de kategoriktir.
• Evlerde kullanılan enerji kaynağı (doğalgaz / elektrik / güneş enerjisi …) ve
  Tasarruf etme durumu (ediyor / etmiyor)
  → Kategorik iki değişkendir.

Bu nedenle şemadaki bağlamlar, iki kategorik değişken arasındaki ilişkiyi incelemek için veri toplamayı gerektirir. İlişkinin olup olmadığını anlamak ancak veriyle mümkündür.

b) Farklı istatistiksel bağlamları Şema 2.1’de boş bırakılan kutucuklara yazınız. Yazdığınız istatistiksel bağlamları sınıfta paylaşınız. Belirlediğiniz bu bağlamları veri toplamayı gerektirip gerektirmeme ölçütüne göre sınıf arkadaşlarınızla tartışınız.

Sağlık kategorisi için boş kutu önerisi:

• Beslenme alışkanlığı ile vücut kitle indeksi arasındaki ilişki
• Uyku süresi ile dikkat dağınıklığı arasındaki ilişki

(Bunlar veri toplamayı gerektirir: uyku süresi → kategorik yapılabilir, dikkat durumu → düşük / orta / yüksek gibi sınıflandırılabilir.)

İklim kategorisi için boş kutu önerisi:

• Bölgelere göre sıcaklık türleri arasındaki ilişki
• Nem oranı düzeyi ile mevsim arasındaki ilişki

Eğitim kategorisi için boş kutu önerisi:

• Okul türü ile öğrenci memnuniyeti arasındaki ilişki
• Ders çalışma yöntemi ile sınav başarı durumu arasındaki ilişki

Çevre kategorisi için boş kutu önerisi:

• Atık türü ile geri dönüşüm oranı arasındaki ilişki
• Bölgedeki ulaşım türü ile hava kirliliği düzeyi arasındaki ilişki

Doğa kategorisi için boş kutu önerisi

• Toprak türü ile bitki çeşitliliği arasındaki ilişki
• Hayvan türü ile yaşam alanı arasındaki ilişki

Bu bağlamlar veri toplamayı gerektirir mi?

Evet; çünkü bağlamların çoğu yine iki kategorik değişkenin ilişkisini incelemeyi amaçlar.
Örneğin:

• Toprak türü (kategorik)
• Bitki çeşitliliği sınıfları (kategorik)

Bu tür ilişkiler ancak gerçek verilere dayanarak değerlendirilebilir. Öğrenciler, sınıfta bu bağlamların veri toplamaya uygun olup olmadığını, örneğin:

• Veri bulunabilirliği
• Değişkenlerin sınıflandırılabilir olup olmaması
• Gerçek yaşamda ilişki araştırılabilirliği

gibi açılardan tartışabilirler.

10. Sınıf Matematik Ders Kitabı Cevapları (MEB Yayınları)