10.sınıf matematik ders kitabında sayfa 88 deki sinüs-kosinüs ve sinüs alan teoremleri ile ilgili alıştırma sorularının cevapları, detaylı çözümleri
Trigonometri gözünüzü korkutmasın! Kosinüs Teoremi, Sinüs Teoremi ve Sinüs Alan Formülü arasındaki bu ince farkları anladığınızda, üçgen geometrisinin ne kadar mantıksal ve çözülebilir olduğunu göreceksiniz. Her üç teoremle ilgili aşağıya daha detaylı bilgi ekledik. Hem teoremlerin ne olduğunu hem de hangisinin ne zaman kullanıldığını öğrenmek isterseniz mutlaka okuyunuz.
10.Sınıf Matematik Ders Kitabı Sayfa 88 Cevapları – Alıştırmalar
1. Aşağıdaki görselde bir arkeoloji kazısında ortaya çıkarılan iki antik heykel kalıntısının üçgen şeklinde taş duvar ile çevrilmiş olduğu düşünülmektedir.
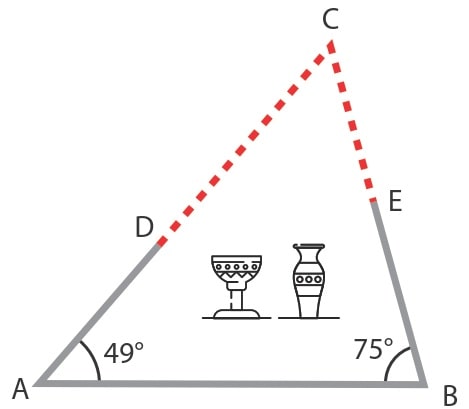
Taş duvarın bir kısmı kazı sırasında ortaya çıkarılmış, henüz kazı yapılmamış kısım kesik çizgilerle gösterilmiştir. Kazı sırasında ortaya çıkarılmış duvarların uzunlukları |DA| = 10 m, |AB| = 24 m, |BE| = 12 m olup duvarlar arasındaki
açıların ölçüleri 49° ve 75°dir. (Hesaplamalarınızda duvar kalınlığını göz ardı ediniz. sin49° . 0,7 sin56° . 0,8 sin75° . 0,9 alınız.)
Buna göre
a) Kazı yapılarak ortaya çıkarılması beklenen duvarlardan DC kısmının uzunluğunun kaç metre olduğunu bulunuz.
Çözüm:
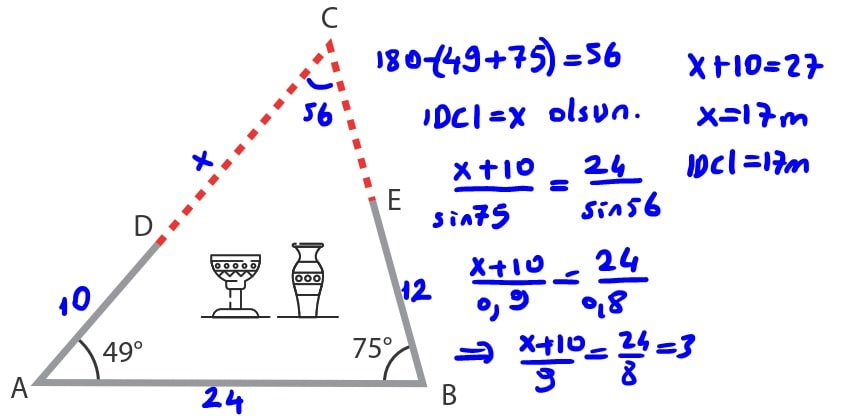
b) Kazı yapılarak ortaya çıkarılması beklenen duvarlardan CE kısmının uzunluğunun kaç metre olduğunu bulunuz.
Çözüm:
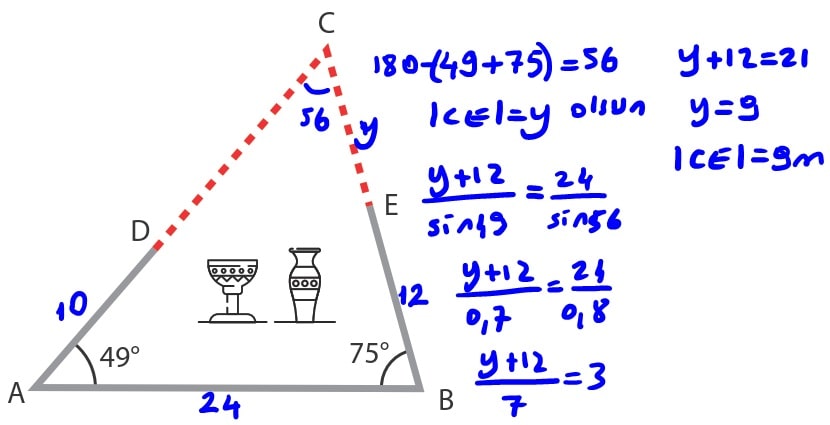
c) Her 1 metre duvar kazısı için 4 işçinin her birinin 8 saat çalışması gerekmekte ve her işçinin 1 saatlik çalışma ücreti 100 TL’dir. Buna göre kazının kalan kısmının kaç saatte biteceğini ve kazının kalan kısmı için işçilere ödenecek ücretin kaç TL olduğunu bulunuz.
Çözüm: Kazının kalan kısmı x+y=9+17=26 m, 1 metre için 1 işçi 4.8=32 saat çalışır. Böylece 1 metre için 32.100 = 3200 TL ücret 1 metre 32 saatte biterse 26 metre, 26.32 = 832 saatte biter. 832.100 = 83.200 TL ödenir.
2. Jalon: Arazi ölçümlerinde noktaların geçici olarak işaretlenmesi ve karşıdan görülmesini sağlayan metal veya tahta çubuklardır. Bitki örtüsünün rahat görüşü engellediği durumlarda jalonların üstüne flama asılır.
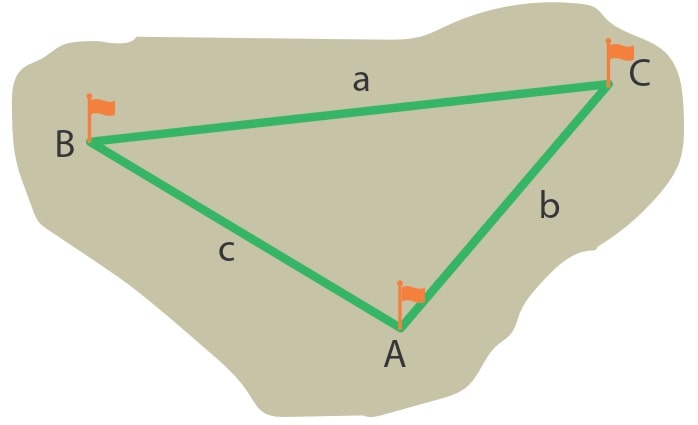
Bir harita mühendisi krokisini çıkarmak istediği arazide A, B, C noktalarına jalonları yerleştirerek noktalar arasındaki uzaklıkları ve iki doğru parçası arasındaki açıların ölçülerini tespit etmiştir. Ölçüm sonuçlarını bir kâğıda yazmış fakat kâğıdın bir kısmı yıpranarak bazı ölçüm sonuçları okunamaz hâle gelmiştir.
Buna göre
a) B ve C noktalarına yerleştirilen jalonlar arasındaki mesafenin bilinmemesi durumunda hangi açı ölçüleri ve kenar uzunlukları bilinirse |BC| = a uzunluğu bulunabilir? Kullanacağınız teoremi de belirterek cevabınızı aşağıdaki alana yazınız.

b) B ve C noktalarına yerleştirilen jalonlar arasındaki mesafenin bilinmemesi durumunda alanı bilinen ABC üçgeninin hangi açı ölçüleri ve kenar uzunlukları bilinirse |BC| = a uzunluğu bulunabilir? Kullanacağınız teoremi de belirterek cevabınızı aşağıdaki alana yazınız.

Kosinüs Teoremi:
Kosinüs Teoremi, herhangi bir üçgende, kenar uzunlukları ile açıların kosinüs değerleri arasındaki ilişkiyi kuran temel bir prensiptir. Bu teorem, özellikle bir üçgenin dik üçgen olması zorunlu olmadığında devreye girer ve ünlü Pisagor Teoremi’nin genel bir hali olarak düşünülebilir.
Kosinüs Teoremi’nin iki temel kullanım amacı vardır:
- Üçüncü Kenarı Bulmak: Bir üçgenin iki kenar uzunluğu ve bu iki kenar arasındaki açı biliniyorsa, teorem yardımıyla üçüncü kenarın uzunluğu hesaplanabilir.
- Açıyı Bulmak: Eğer bir üçgenin tüm kenar uzunlukları biliniyorsa, teorem kullanılarak herhangi bir açının kosinüs değeri ve dolayısıyla açının kendisi bulunabilir.
Özetle, Kosinüs Teoremi üçgenin kenar uzunlukları arasındaki metrik ilişkiyi açılar üzerinden açıklamaktadır.
Sinüs Teoremi:
Sinüs Teoremi, bir üçgenin kenar uzunlukları ile bu kenarların karşısındaki açıların sinüs değerleri arasında sürekli bir orantı olduğunu ifade eder. Bu teorem, bir üçgendeki her kenar uzunluğunun, o kenarı gören açının sinüs değerine bölünmesiyle elde edilen sonucun tüm kenarlar için aynı olduğunu belirtir.
Bu orantı sabiti, aynı zamanda üçgenin çevresinden geçen çemberin (çevrel çember) çapına eşittir. Sinüs Teoremi’nin yaygın kullanım alanları şunlardır:
- Bilinmeyen Kenarı Bulmak: Bir kenar uzunluğu ve iki açının ölçüsü bilindiğinde diğer kenarların uzunlukları hesaplanabilir.
- Bilinmeyen Açıyı Bulmak: İki kenar uzunluğu ve bir açının ölçüsü bilindiğinde, diğer açının sinüs değeri ve dolayısıyla açının kendisi bulunabilir.
Sinüs Teoremi, üçgenin kenarları ve açıları arasındaki oransal dengenin temelini oluşturur.
Sinüs Alan Formülü
Sinüs Alan Formülü, bir üçgenin alanını hesaplamak için kullanılan pratik bir yöntemdir. Geleneksel olarak alan hesaplaması için yükseklik bilinmesi gerekirken, bu formül sayesinde yükseklik bilgisine ihtiyaç duyulmaz.
Formülün temel prensibi, bir üçgenin alanının, iki kenar uzunluğunun çarpımı ile bu iki kenar arasındaki açının sinüs değerinin çarpımının yarısına eşit olmasıdır. Bu sayede, sadece iki kenar ve aralarındaki açının ölçüsü bilindiğinde, üçgenin kapladığı düzlemsel büyüklük (alan) kolaylıkla hesaplanabilir. Bu formül, özellikle geometri problemlerinde ve gerçek yaşamdaki alan hesaplamalarında büyük kolaylık sağlar.
10. Sınıf Matematik Ders Kitabı Cevapları (MEB Yayınları)
[…] 10.Sınıf Matematik Kitabı Sayfa 88 Cevapları – Alıştırmalar […]