10.Sınıf matematik ders kitabında Sayfa 87 de kosinüs ve sinüs teoremlerinin günlük hayatta nelerde kullanılabildiği ile ilgili yeni müfredata uyumlu 21.Sıra Sizde sorusunun cevabı ve ayrıntılı çözümleri
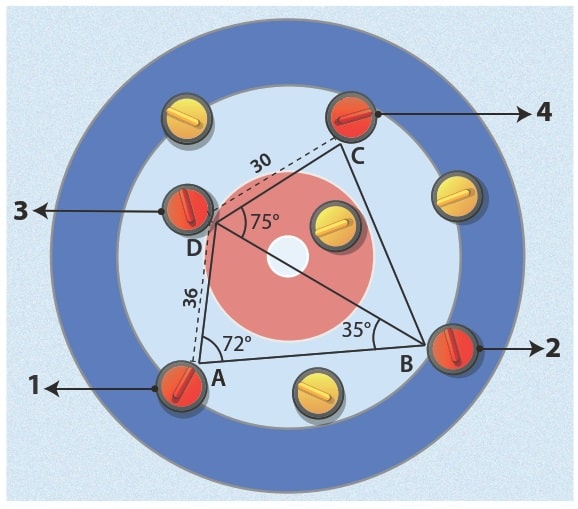
Curling (körling), buz bir pist üzerinde oynanan takım oyunudur. Oyunda iki farklı renkte taş kullanan takımlar iç içe geçmiş halkalardan oluşan ‘’ev’’ adı verilen hedefin merkezinde taşları durdurmayı amaçlar.
Bir körling antrenmanı sırasında yapılan atışlar sonrasındaki taşların ‘’ev’’ içinde durdukları son noktalar görselde veriliyor. Takım antrenörü atış analizi yapabilmek amacıyla kırmızı taşlar üzerinde belirlediği noktalar arasındaki uzunlukları ölçerek kaydediyor. Taktik tahtasına görseldeki gibi taşların son konumlarını çizerek ölçtüğü bazı uzunlukları ve açı ölçülerini yazıyor.
Görsel üzerinde verilenleri dikkate alarak soruları cevaplayınız.
(sin 35° = 0,57 sin 72° = 0,95 cos 75° = 0,2 alınız.)
a) 2 ve 4 numaralı taşların belirlenen noktaları arasındaki uzaklığının yaklaşık kaç cm olduğunu bulunuz.
Çözüm:
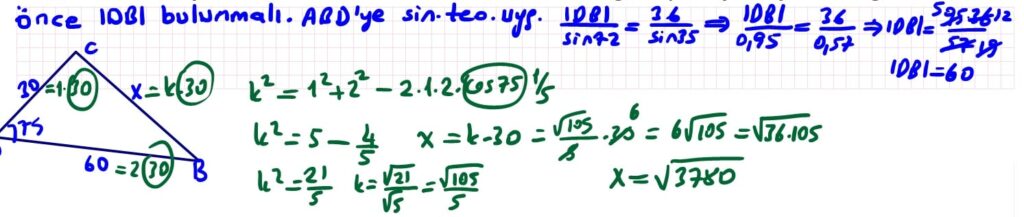
b) 2 ve 4 numaralı taşların belirlenen noktaları arasındaki uzaklığı bulmak için uyguladığınız adımları, varsa kullandığınız özellik veya teoremi belirterek yazınız.
Cevap: ①②③ numaralı taşlardan oluşturulan üçgende sinüs teoremi kullanılarak ②③ numaralı taşlar arasındaki IDBI uzaklığını, daha sonra ②③④ numaralı taşlardan oluşturulan üçgende kosinüs teoremini kullanarak ②④ numaralı taşlar arasındaki IBCI uzaklığını bulduk.
c) Sinüs ve kosinüs teoremlerinin hangi durumlarda kullanıldığı ile ilgili fikirlerinizi aşağıdaki alana yazınız.
Cevap: Bu iki teorem, dik olmayan (eğik) üçgenlerde eksik kenar ve açıları bulmak için kullanılır. Sinüs teo, en az iki açı ve bir kenar bilindiğinde (AAK veya KAA durumları) , veya bir kenar ve karşısındaki açı çifti tam bilindiğinde diğer kenarı bulmak için kullanılır. Kosinüs teoremi; İki kenar ve aradaki açı bilindiğinde (KAK durumu) üçüncü kenarı bulmak Veya üç kenar bilindiğinde (KKK durumu) herhangi bir açıyı bulmak için kullanılır.
10. Sınıf Matematik Ders Kitabı Cevapları (MEB Yayınları)
[…] 10.Sınıf Matematik Kitabı Sayfa 87 Cevapları- Sinüs-Kosinüs Teoremi […]