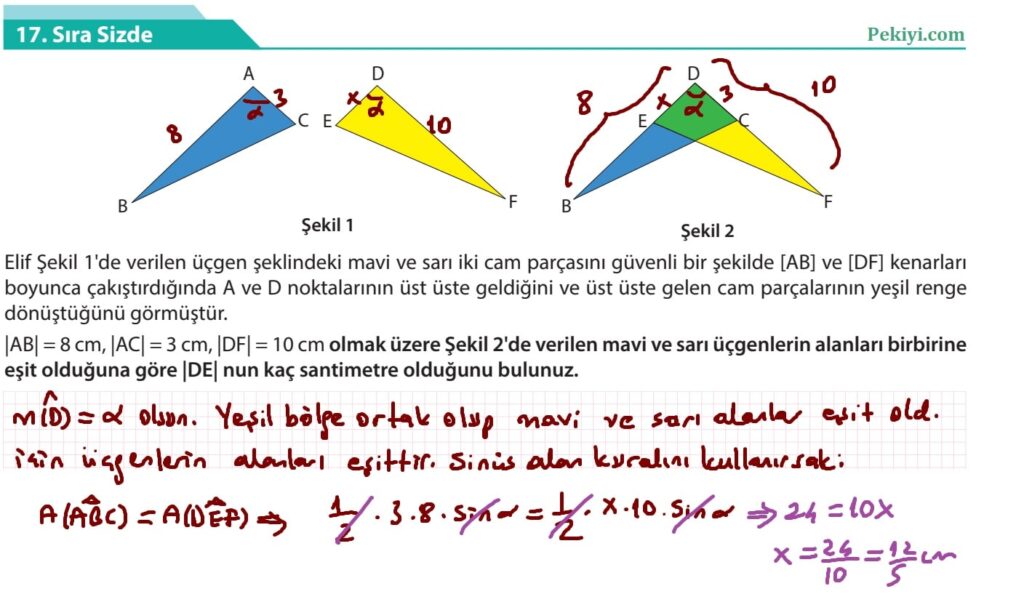
MEB yayınları 10.Sınıf Matematik ders kitabında sayfa 74 deki sinüs alan formülü ile ilgili 17.Sıra Sizde sorusunun cevabı, detaylı çözümü burada
Bir üçgenin alanını bulmanın en kullanışlı yollarından biri sinüs alan kuralıdır. Bir üçgenin iki kenarının uzunluğu ve bu iki kenar arasındaki açının ölçüsünün bilindiği durumda üçgenin alanı bulmada kullanılan şu formüle sinüs alan kuralı denir:
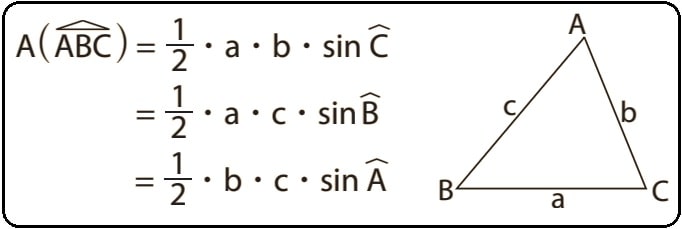
Üçgende sinüs alan formülü, bir üçgenin alanını hesaplamanın alternatif bir yoludur. Normalde bir üçgenin alanını bulmak için taban uzunluğunu ve o tabana ait yüksekliği bilip bunları çarpıp ikiye böleriz. Ancak bu formül, yükseklik bilgisinin olmadığı veya yüksekliği bulmanın zor olduğu durumlarda çok kullanışlıdır. Tabi verilen açının sinüs değeri bilinmelidir.
10.Sınıf Matematik Kitabı Sayfa 74 Cevabı-Çözümü- MEB Yayınları
🔹 Sinüs Alan Formülü Kullanım Alanları
- İki kenar ve aralarındaki açı (2K1A) biliniyorsa alanı kolayca bulmak için.
- Trigonometrik sorular ve sinüs teoremiyle bağlantılı çözümlerde.
- Gerçek yaşam problemleri: Harita, mühendislik veya navigasyonda üçgen ölçümlerinde.,,
Bu yöntem, üçgenin herhangi iki kenarını ve bu iki kenarın arasında kalan açıyı kullanır. Üçgenin alanını bulmak için, seçtiğimiz bu iki kenarın uzunluklarını birbiriyle çarparız. Ardından, aralarındaki açının sinüs değerini buluruz. Bulduğumuz bu sinüs değerini, kenar uzunluklarının çarpımıyla çarparız. Son olarak, bu çarpımın sonucunu ikiye böleriz.
Basitçe ifade etmek gerekirse: İki kenar çarpılır, aralarındaki açının sinüsü ile tekrar çarpılır ve sonuç ikiye bölünür.
Sinüs Alan Kuralı Nerede Kullanılır ve Kolaylık Sağlar:
- Yüksekliğin Bilinmediği Durumlar: En büyük kullanım alanı budur. Bir üçgende taban ve yüksekliği bulmak yerine, iki kenar uzunluğu ve aralarındaki açıyı bildiğimizde, doğrudan alanı hesaplayabiliriz. Bu, özellikle üçgenin karmaşık konumlarda olduğu veya sadece kenar-açı bilgilerinin verildiği sorularda büyük kolaylık sağlar.
- Kenar ve Açı İlişkileriyle Alan Hesabı: Trigonometri ve geometri problemlerinde, alanı sadece kenar uzunlukları veya açılar üzerinden ifade etmemiz gerektiğinde bu formül devreye girer.
- Bilinmeyen Uzunlukları Bulmada: Bazen üçgenin alanı ve diğer bazı bilgileri verilmiştir. Bu formül sayesinde, bilinmeyen bir kenar uzunluğunu veya bir açının sinüs değerini (dolayısıyla açının kendisini) bulmak için ters işlem yapma imkanı doğar.
Özetle, üçgenin yüksekliğini çizme ve hesaplama zahmetine girmeden, sadece iki yan yana kenarı ve aralarındaki açıyı kullanarak hızlıca alanına ulaşmayı sağlayan pratik bir yoldur. Soruların çözümünü, bilmediğimiz bir yüksekliği bulma zorunluluğunu ortadan kaldırarak hızlandırır ve basitleştirir.
10. Sınıf Matematik Ders Kitabı Cevapları (MEB Yayınları)
[…] 10.Sınıf Matematik Kitabı Sayfa 74 Cevabı – Sinüs Alan Formülü […]